
One note of caution when looking at economic data that extends over decades in time check if they have been adjusted for inflation. Is there a long-term trend? For example, in the consumer spending data, we can see a long-term generally upward trend since the end of the recession in June 2009.
#Interpreting mean and standard deviation excel bar graphs series#
When looking at a time series plot like Figure 4.7 it is important to examine and interpret some key basic features: Further, since the distribution is symmetric we would have 16% (half of the 32%) falling below 62.3 inches and another 16% falling above 70.3 inches. Since 68% of the heights are within one standard deviation of the mean, the remaining 32% would fall outside of that. One would expect it to be very unusual for someone in this sample to be smaller than 54.3 inches or taller than 78.3 inches. 99.7% of the heights lie between 54.3 and 78.3 inches.95% of the heights lie between 58.3 and 74.3 inches.
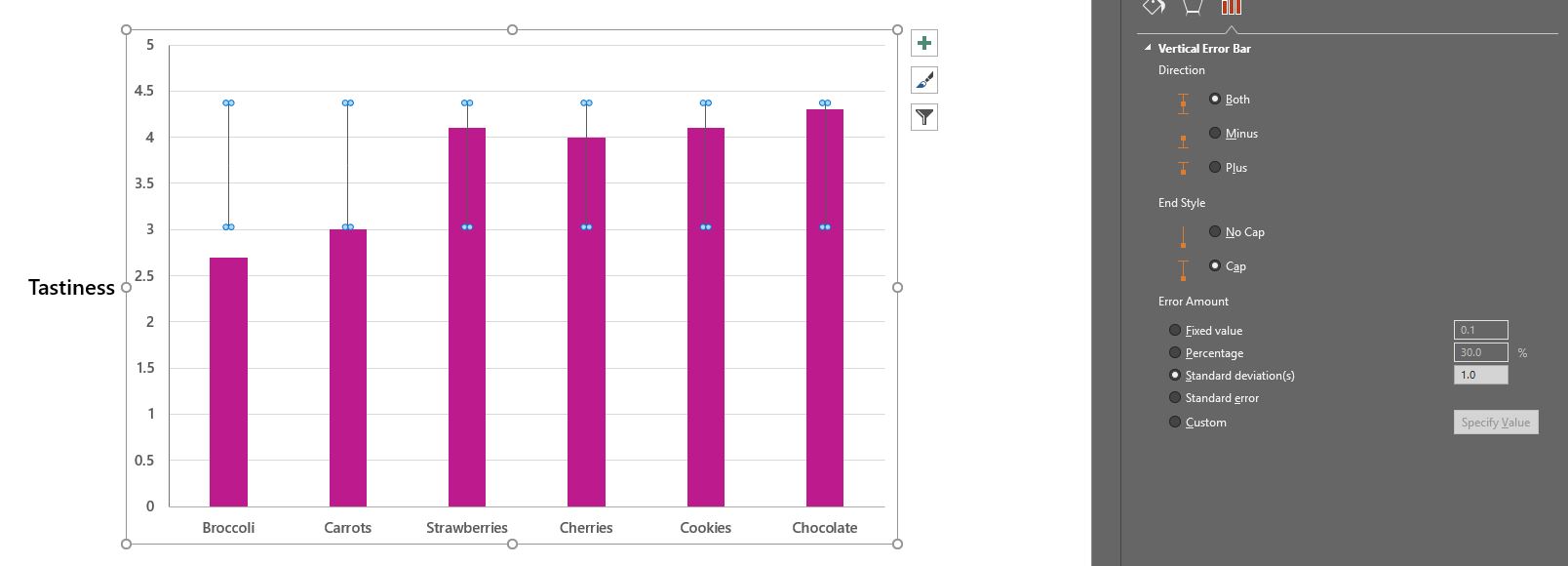
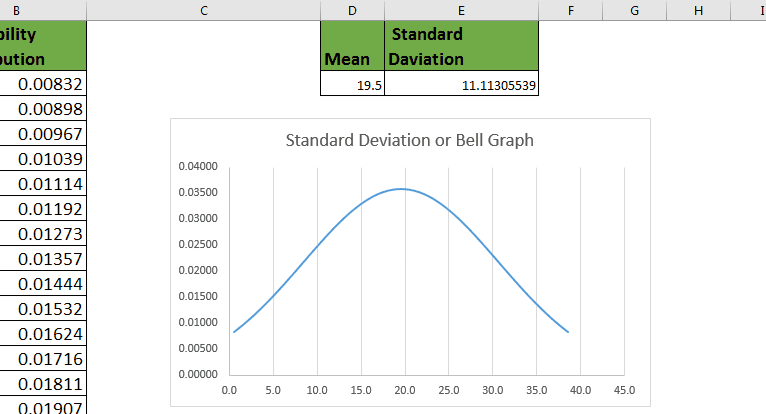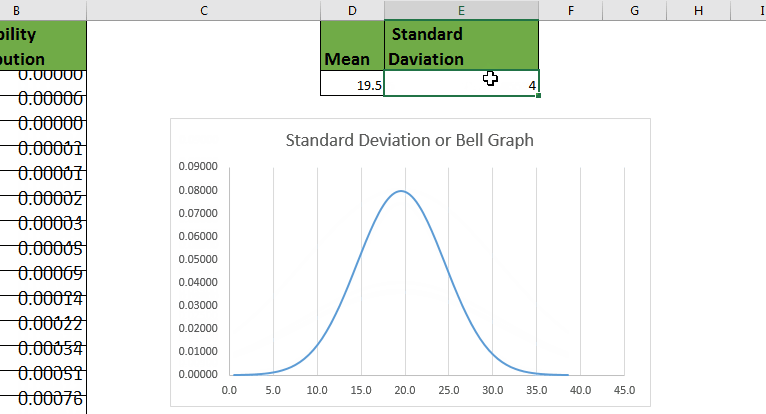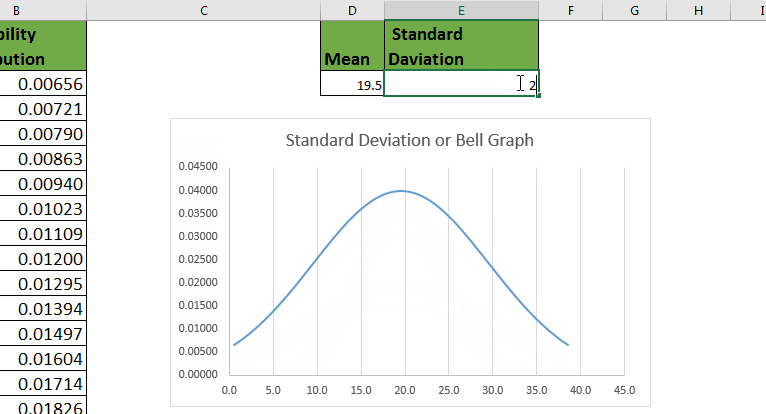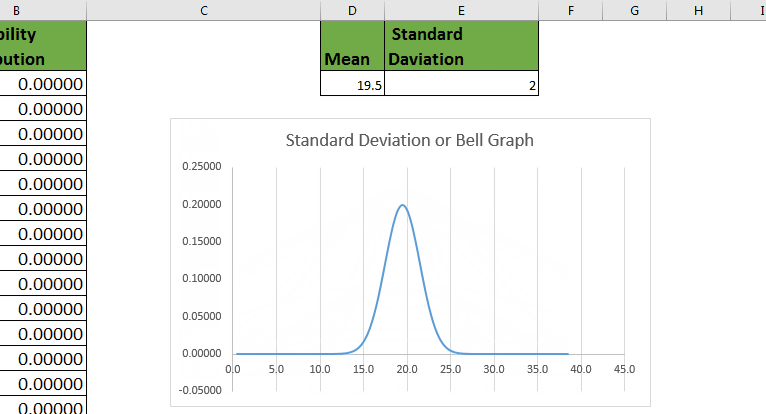
The mean and standard deviation (SD) for this sample is 66.3 inches and 4 inches, respectively. Recall the variable heights used in Example 4.3. Since the histogram shows that this data is normally distributed, the empirical rule can be applied. The distributions of such measures within a homogeneous group of people will then approximately follow a normal curve Many measures used by psychologists to gauge levels of characteristics like stress or anxiety or happiness are based on questionnaires that score your answers to lots of individual questions and then sum them up to get a final measure. Thus, the distribution of the weights of cartons of large eggs at a grocery store will look like a normal curve because the weight of a carton arises from the sum of the weights of the dozen eggs inside. It can be shown that variables that arise as a result of the sum or average of a fixed number of individual smaller components of a similar nature will have this shape. Data that has this pattern are said to be bell-shaped or have a normal distribution. The predictable pattern of interest is a type of symmetry where much of the distribution of the data is clumped around the center and few observations are found on the extremes. Many measurement variables found in nature follow a predictable pattern. How are two measurement variables associated? How do percentages or averages change over time? How do the distributions of two measurement variables compare?

How is a categorical variable distributed? (normal or bell-shaped curve is a special case) How are all of the numbers on a list distributed over the number line? What is the relative standing of an individual value compared with other numbers on a list?
Where are values located along the number line? An overview of some key questions addressed is given in the table below. In Lesson 4 we continue our discussion of describing data through numerical summaries and also think about statistical pictures.


 0 kommentar(er)
0 kommentar(er)
